Gentle introduction into compilers. Part 1: Lexical analysis and Scanner

My journey into compilers world started with this tweet and the question how does Angular AOT compilation that uses static code analysis work. After some debugging I found out that it relies heavily on TypeScript compiler so the quest then began to reverse-engineer it. What’s interesting is that most compilers are implemented using the same principles collectively known as compilers theory. Having a good grasp of this theory is indispensable when trying to understand a compiler internals.

This article is the first in the series that will summarize everything I learnt along the way. Here I’ll describe the concepts important for understanding the first stage of every compiler — lexical analysis.

The article contains the bare minimum of theory and formalism but it still turned out to be mostly theoretical. In the last chapter I show how TypeScript scanner is implemented and provide relevant links.

TypeScript grammar is based on the ECMAScript (JavaScript) spec and I hope you’ll get curios enough to follow the links in the article and get familiar with the spec. If you do that you should be able to understand the grammar and learn the syntax of the upcoming JavaScript features long before it’s explained on MDN. If you make it to the end of the article you can test yourself by trying to understand the syntax of the decorators feature described in the decorator spec.

The article is quite lengthy and hence not meant to be read in one go. Read it bit by bit and allow time for the concepts to settle in your head. If you always wanted to learn how to read the ECMAScript spec or understand how a compiler (scanner) works this article is for you.

Common Stages

Compilers are computer programs that translate a program written in one language into a program in another language. A compiler must first understand the source-language program that it takes as input and then map its functionality to the target-language program. Because of the distinct nature of these two tasks it makes sense to split compiler functionality into two major blocks: a front-end and a back-end. The main focus of the former is to understand the source-language program, while the latter focuses on transforming it into the target-language program.

Each block is comprised of a sequence of several phases with each stage taking input from its previous stage, modifying it and producing its own representation of source program and passing it to the next phase. The front-end includes three main stages called lexical, syntax and semantic analysis. The first phase takes the source code as a stream of characters and identifies distinct words (tokens) such as variable names, keywords and punctuators. The second phase determines the validity of syntactic organization of the program and produces Abstract Syntax Tree (AST). Semantic analysis checks whether the AST follows the rules of a language (type checking, name resolution).

This article is concerned with the first stage of lexical analysis and its main acting character scanner, a.k.a recognizer.

Formal languages and grammar

Before we get to the scanner implementation it’s important to talk a little about natural and formal languages and their grammars. Natural languages, like English or French, are used mostly for communication and evolved naturally. Formal languages, on the hand, are languages that are designed by people for specific applications — programming languages to express computations, mathematical notation to denote relationships among numbers etc.

Both natural and formal languages can be described by a grammar. A grammar is a set of rules that describe how to put together a sequence of symbols like characters, words (tokens) or sentences (statements) that are valid according to the language’s syntax. The grammar of natural languages is incredibly complex and is discovered through empirical investigation. On the other hand, the grammar of formal languages (formal grammar) is usually pretty simple and is defined however we need. Depending on what type of symbols we want to define rules for we can distinguish several types of grammar.

Lexical grammar describes the structure of a language vocabulary, that is, every token (word) that can be used in the language. For example, in JavaScript both \ and d are in the alphabet of the language, but the grammar doesn’t define any rule where \ immediately followed by d can be recognized as a valid token outside of a regular expression literal and so if you execute the following code \d you will get the invalid token syntax error:\d
Uncaught SyntaxError: Invalid or unexpected token

Syntactical grammar defines the structure of the language, that is, the way the tokens (words) can be arranged to form statements (sentences). For example, JavaScript lexical grammar defines two tokens var and const but there’s no rule that states that var can be followed by const and so if you execute the following code you will get the unexpected token syntax error:var const
Uncaught SyntaxError: Unexpected token const

It is structurally illegal statement according to ECMAScript syntactical grammar and so the compiler doesn’t expect the token const to follow the token var in the statement we wrote before. Also notice the unexpected versus invalid difference in the error messages.

Lexical analysis

Lexical analysis is the first stage of a three-part process that the compiler uses to understand the input program. The role of the lexical analysis is to split program source code into substrings called tokens and classify each token to their role (token class). The program that performs the analysis is called scanner or lexical analyzer. It reads a stream of characters and combines them into tokens using rules defined by the lexical grammar, which is also referred to as lexical specification. If there are no rules that define a particular sequence of characters the scanner reports an error. This is exactly what happened with our example string \d that produced Invalid or unexpected token syntax error.

For each recognized token a scanner assigns a syntactic category based on the grammar. The list of categories or token classes for ECMAScript is quite extensive and contains among others such classes as Identifier, NumericLiteral and StringLiteral and various keywords like ConstKeyword, LetKeyword and IfKeyword.

So usually the output of the lexical analysis stages is the sequence of tokens where each token has an associated class and substring usually referred to as lexeme:

ConstKeyword

If you’re curios what kind of tokens are defined by ECMAScript check the SyntaxKind enumeration (until the // Parse tree nodes comment) in the TypeScript implementation.

Lexical analyzer can be implemented to scan the entire source program and produce a complete sequence of tokens or to perform a gradual scan and recognize one token at a time. The scanner that converts the whole source program into an array of tokens before a parser runs is pretty uncommon since it needlessly consumes memory. So scanners are usually implemented to produce tokens only when requested by a parser, which is the case with TypeScript scanner as well. The TS scanner is also interesting in another way. The JavaScript syntax defines a few language constructs, like regular expressions and templates literals, that introduce parsing ambiguity so it becomes possible for the scanner to recognize different set of tokens depending on the parsing context. Since this parsing context is defined by the parser when requesting a token the TS scanner in a way can be called parser-driven. I’ll explain this intricacy of the language in the Multiple goal symbols section.

Defining tokens

Let’s use a familiar case of declaring a variable in JavaScript to demonstrate how grammar rules work. In JavaScript we can declare a variable using const declarations like this:const v = 3

Let’s assume for simplicity the initialization value can only be a numeric literal. When you look at the source code you clearly see the const word declaring a variable v , the assignment operator = and the numeric literal 3 used as an initialization value for the variable. Unsurprisingly, the scanner doesn’t see it that way. Since the ECMAScript defines a program source using Unicode symbols the compiler sees the following sequence of code points:c o n s t v = 3
99, 111, 110, 115, 116, 32, 118, 32, 61, 32, 51

Now its job is to split the expression into tokens and categorize them so the following list of tokens is produced:{class: SyntaxKind.ConstKeyword, lexeme: 'const'}
{class: SyntaxKind.Identifier, lexeme: 'v'}
{class: SyntaxKind.EqualsToken, lexeme: '='}
{class: SyntaxKind.NumericLiteral, lexeme: '3'}

And if we had let instead of the const the first token would be SyntaxKind.LetKeyword. You can click on the token class to see where they are defined in the TypeScript sources. Once token is recognized the scanner stores its value (lexeme) in the tokenValue property which can be accessed using getTokenValue method.

Regular grammar

ECMAScript defines the rules for recognizing an input of Unicode symbols as tokens using regular grammar. According to the Chomsky classification of grammars regular grammar is the most restrictive type with the least expressiveness power. It’s only suitable to describing how the tokens can be constructed but can’t be used to describe sentence structure. However, more restrictions on the grammar make it easier to describe and parse. And since we’re concerned with defining and parsing tokens in this chapter this is the ideal grammar to use.

In the next article in the series we’ll get familiar with the context-free grammar (type 2). This type of grammar allows recursive constructs and is used to define the structure of the program (statements). The other two categories of grammar from the Chomsky classification— unrestricted and context-sensitive grammars — are more powerful than type 2 and 3, but they are far less useful since we cannot create efficient parsers for them.

It’s important to note that most educational materials do not use regular grammar when explaining scanners and instead they define the lexical specification using regular expressions. However, since ECMAScript uses regular grammar for that purposes I’ll be explaining it in this article.

Getting familiar with the grammar

Now, let’s try to see how we can construct the grammar and the rules that help TypeScript identify the list of tokens I showed above. Here it is again and we need to define rules for recognizing each token in the statement:const v = 3{class: SyntaxKind.ConstKeyword, lexeme: 'const'}
{class: SyntaxKind.Identifier, lexeme: 'v'}
{class: SyntaxKind.EqualsToken, lexeme: '='}
{class: SyntaxKind.NumericLiteral, lexeme: '3'}

Each rule in a grammar is defined using productions. A production is a replacement rule specifying possible substitutions that can be recursively performed to generate new symbol sequences. In JavaScript we can declare a variable using either const or let token so we can define the following rule for the symbol Keyword:Keyword ::
const
let

The rule for the symbol Keyword has two productions (production rules) stating that the symbol Keyword can be replaced either by const or let strings. The Keyword is a synthetic variable called nonterminal symbol meaning that it has productions and can be replaced (the process of replacements doesn’t terminate with it). The replacements are usually referred to as derivations. The productions const and let that this symbol has are called terminals because they don’t have any derivations. The terminal symbols which don’t have any productions are the actual strings that can be found in the source program. The synthetic non-terminal symbols are used in the grammar only to define replacements rules and are never recognized in the source program as valid tokens. ECMAScript defines many other productions for the non-terminal symbol Keyword such as: if, else, for, do, while, function, class etc.

To define grammar ECMAScript uses the following arbitrary form:non_terminal_symbol ::
symbol1 symbol2 (production rule 1, Symbol1 followed by Symbol2)
symbol3 symbol4 (production rule 2, Symbol3 followed by Symbol4)

The symbol to the left of the :: is called left-hand side and the symbol to the right — right-hand side. For the regular and context-free grammars you can only have a non-terminal symbol on the left-hand side of the production rule. The right-hand side can specify both terminals and non-terminals, however the regular grammar is restricted to have either:

• only terminals
• or terminals and a single non-terminal that’s always at the beginning (left-linear) or always at the end (right-linear):non_terminal_symbol ::
  terminal_symbolnon_terminal_symbol ::
  terminal_symbol non_terminal_symbol (right-linear)non_terminal_symbol ::
  non_terminal_symbol terminal_symbol (left-linear)

The context-free grammar is more relaxed and allows any number of terminals and non-terminals on the right-hand side. Both RG and CFG can have any number of alternations (productions) for each left-hand side symbol:non_terminal_symbol ::
production rule 1
production rule 2
...
production rule n

There are also other grammar notations like Backus–Naur form (BNF) that uses the following syntax:nonterminal_symbol ::= symbol1 | symbol2

so our grammar rule for the Keyword would be written as:Keyword ::= const | let

Other alternative notations replace the ::= with -> so the rule looks like this:Keyword -> const | let

In this regard ECMAScript uses its own arbitrary format explained above. The details of grammar notation are described in the Grammar Notation section and I strongly suggest reading it. Here are some important parts:

Terminal symbols …are shown in fixed width font, nonterminal symbols are shown in italic type… One or more alternative right-hand sides for the nonterminal follow on succeeding lines… The definition of a nonterminal is introduced by the name of the nonterminal followed by one or more colons. ECMAScript uses double semicolon to denote lexical grammar and single semicolon for the syntactic grammar.

Applying production rules

A production rule is applied to a symbol by replacing one occurrence of the production rule’s left-hand side by that production rule’s right-hand side. This is a bit wordy so let’s see an example. Suppose you want to define a language of reserved words. The grammar for such language will start with the non-terminal symbol ReservedWord. ECMAScript defines the following productions for it:ReservedWord ::
Keyword
FutureReservedWord
NullLiteral
BooleanLiteral

but let’s limit ourselves to only Keyword now:ReservedWord ::
Keyword

Earlier we defined the grammar for the Keyword like this:Keyword ::
const
let

So by first replacing ReservedWord with Keyword and then replacing Keyword with its productions we can end up with the language that has two words — const and let. We would call such a language finite since it can contain at most 2 different strings. All existing languages are infinite because the number of combinations they can contain is potentially infinite. We will see soon why that happens when we’ll be taking a look at the identifier grammar.

In our grammar above the ReservedWord is called start symbol because that’s the symbol we started generating strings from. ECMAScript grammar defines multiple start symbols and calls them goal symbols. I’ll explain later in the article why that is required.

The process that allowed us to start from the start symbol ReservedWord and arrive at the string const or let is called derivation. A derivation of a string for a grammar is a sequence of grammar rule applications that transforms the start symbol into the string. A derivation proves that the string belongs to the grammar’s language. For example, we know that const is a valid expression because ReservedWord can be expanded into Keyword and each Keyword can be expanded into the string const or let.

Recursive nature of the grammar

The recursive nature of the grammar can be demonstrated using variables names usually referred to as identifiers in the context of compilers. As you already know in our example const v = 3 the variable name v is recognized as Identifier. The Identifier is defined by ECMAScript as:Identifier ::
IdentifierName but not ReservedWord

It basically tells us that reserved words is the subset of IdentifierName hence the rules for recognizing identifier names and reserved words are the same. It means that once the scanner recognized the IdentifierName it should we mark it as an Identifier if it’s not in the reserved word, otherwise it is assigned a pertinent class from the ReservedWord category. This is precisely what TypeScript compiler does in the getIdentifierToken function. The reserved words list is comprised of mostly keywords like const, let,if, else, for etc. that we’ve seen above plus null, true and false literals.

So how can the grammar be defined for the IdentifierName? You probably know that some characters like numbers can’t occur at the beginning of the variable name while the name itself can contain a much broader character set including numbers. So there’s a need to separate what the name can start with and what it can continue with. Because of that the grammar needs to be defined using two non-terminal symbols in the sequence:IdentifierName ::
IdentifierStart IdentifierPart

It’s important that both IdentifierStart and IdentifierPart denote a single character from the set of Unicode code points used in the respective positions of the identifier name. I won’t go into details here but if you’re curios read Valid JavaScript variable names in ECMAScript 5. And since both IdentifierStart and IdentifierPart are expanded into a single character from the defined alphabets the above definition states that any IdentifierName name is two characters long. Which is not what we want. If you look at the ECMAScript grammar you will see the following definition:IdentifierName ::
IdentifierStart
IdentifierName IdentifierPart

Let’s break it down. The first production states that an identifier name can be one character long from the set of characters defined by IdentifierStart. If you derive the second production recursively a few times you will see that it can be expanded into an arbitrarily large number of characters starting with IdentifierStart and continuing with IdentifierPart:IdentifierStart IdentifierPart IdentifierPart … IdentifierPart

That is the case where recursion comes in handy. By recursively replacing IdentifierName with the second IdentifierName IdentifierPart production we can match a string of any length.

It’s interesting to know that some grammar notations introduce not-standard repetition operators like * or {…} that would result in the following grammar:IdentifierName ::
IdentifierStart IdentifierPart*IdentifierName ::
IdentifierStart {IdentifierPart}

Significance of white-space

For some parts of the grammar white-space plays an important role that helps scanner distinguish one token from another. Let’s take a look at the following code and the resulting tokens:newObject
{class: SyntaxKind.Identifier, lexeme: 'newObject'}

Here newObject is assigned the Identifier category. It is done by recursively deriving IdentifierPart production as we saw above and because every character in the word newObject falls into the character set defined for the IdentifierPart symbol the scanner recognizes entire string as a one single token. Here is the other example:new Object
{class: SyntaxKind.NewKeyword, lexeme: 'new'}
{class: SyntaxKind.Identifier, lexeme: 'Object'}

Now although the characters are the same they are parsed as two separate tokens due to the presence of the space. The scanner is able to split the tokens because when deriving the IdentifierPart productions it doesn’t recognize the space as a valid character for the IdentifierPart and produces the token IdentifierName with the lexeme new of 3 characters. It then looks up the new token in the keywords lists and marks it as the NewKeyword (I’ll explain that lookup later).

At other times characters like ( that can’t be used as IdentifierPart help split the tokens:if(s=3){...}
IfKeyword OpenParenToken ...

White-space is also mentioned as a separate token class for the InputElementDiv goal symbol:InputElementDiv::
WhiteSpace
LineTerminator
...

Defining assignment operators and number literals rules

I’ve shown how grammar is defined for the const keyword and the identifier v. Now the only things that’s left is to define rules for is the equals sign and the number 3:ConstToken Identifier = 3

The equals sign is what we use in JavaScript to assign a value to a variable. There are many other assignment operators and they are all conveniently grouped under the AssignmentOperator symbol:AssignmentOperator : one of
*= /= %= += -= <<= >>= >>>= &= ^= |= **=

And the last piece — the number 3. In JavaScript numbers can be represented using many forms: decimal literal with a fraction part 1.58, binary 0b11 or hex 0x11 literals, the exponent form 5e2 etc. It makes sense to group all these under NumericLiteral symbol:NumericLiteral::
DecimalLiteral
BinaryIntegerLiteral
OctalIntegerLiteral
HexIntegerLiteral

These are all non-terminal symbols. You can click on the links to track each non-terminal productions down to the terminal symbols.

Multiple goal symbols

When exploring derivation process we learnt that it starts with the goal (start) symbol. And this is where ECMAScript lexical grammar becomes complicated as it defines several goal symbols. Consider the following code snippet:

/foo/g

If ECMAScript scanner starts taking derivations for the following statement using the primary goal (start) symbol InputElementDiv with the following production rules:InputElementDiv ::
WhiteSpace
LineTerminator
Comment
CommonToken
DivPunctuator
RightBracePunctuator

it will recognize the following stream of tokens:

/             foo            /             g

However, if you’ve been programming in JS sufficiently enough you must know that /foo/g represents regexp literal. So it should be recognized as one RegularExpressionLiteral token using the following grammar rule:RegularExpressionLiteral ::
/ RegularExpressionBody / RegularExpressionFlags

The basic InputElementDiv goal symbol doesn’t have any derivations that can lead a scanner to the RegularExpressionLiteral symbol. So we need to define a new goal symbol InputElementRegExp with the production for the regexp literal:InputElementRegExp ::
WhiteSpace
...
RegularExpressionLiteral

Using this goal symbol the scanner would correctly recognize the /foo/g as RegularExpressionLiteral. But now the question that you might ask is how does a scanner know which goal symbol to use when parsing a token? As I mentioned earlier in the article the goal symbol (context) is set by the parser. The parser requests tokens one by one from the scanner and if the current parsing context allows usage of the InputElementRegExp goal symbol the parser requests the scanner to recognize tokens using this goal symbol.

For example, assume that the parser currently parses PrimaryExpression which has the following grammar:PrimaryExpression :
this
IdentifierLiteral
…
RegularExpressionLiteral

The grammar states that the regular expression literal can be derived from the primary expression so the scanner defines InputElementRegExp goal symbol for the scanner. The TypeScript compiler is implemented to re-scan the current token if it detects that current context allows goal symbols other than primary InputElementDiv. ECMAScript defines a few other goal symbols — to learn more about them see this great StackOverflow answer.

Regular expressions

Sometimes the lexical grammar is specified using repetition operator instead of a recursion. For example, here is how Java 8 grammar defines the IdentifierChars symbol which is equivalent to IdentifierName symbol with recursive productions in EcmaScript:IdentifierChars:
JavaLetter {JavaLetterOrDigit}JavaLetter:
any Unicode character that is a "Java letter"JavaLetterOrDigit:
any Unicode character that is a "Java letter-or-digit"

The parenthesis for the JavaLetterOrDigit is the repetition notation as explained in the grammar doc:

The syntax {x} on the right-hand side of a production denotes zero or more occurrences of x.

This way of specifying the grammar has a special property: by substituting every nonterminal (except the root one) with its righthand side, you can reduce it down to a single production for the root, with only terminals on the right-hand side. This reduced expression can then easily be converted into a regular expression (regex). For example, for the IdentifierChars we would have the following:[range of Java letter][range of Java letter-or-digit]*

Using repetition operator in regular grammar rules instead of a recursive structures is not conventional. If the grammar is specified using standard notation with recursive structures the mechanical conversion of the grammar into regural expressions is not trivial: you first have to convert the grammar into non-deterministic finite automaton (NFA, explained below) and then convert NFA into regural expressions. However, it is often much easier to come up with an equivalent regular expression by applying “logical thinking”.

Both regular grammar and regular expression can describe a sequence of characters drawn from a fixed set and can be used interchangeably. For that reason regular expressions are routinely used to specify the lexical specification instead of regular grammar. For example, this is the case for lexical analyzer (scanner) generators, such as Flex.

Finite automaton

Besides regular grammar and regular expressions there’s another way of specifying lexical specification — finite automata (FA). They are all simply three different formalisms for the doing fundamentally the same thing — recognizing sets of characters. The basic reasons that we have three ways to do that same thing is that they were developed independently. FA, however, provides the best mental model for describing a scanner implementation and we will use it for that purpose.

The automaton can be explained using a character-by-character algorithm to recognize words. Suppose we want to recognize the const token. We need to write code that tests for c followed by o followed by n and so on until we reach the last character t. If we depict each step of the program as a transition diagram we will have the following:

Each automaton has states depicted as circles on the diagram above. In this article I will be talking only about an automaton which has a finite number of states (hence finite automaton). The last state marked with a double line is called an accepting state. An automaton can have any number of accepting states. If after reading an input the automaton ends up in the accepting state, the input is recognized as a valid sequence of characters.

There are two types of finite automaton — deterministic (DFA) and non-deterministic (NFA). The biggest difference between the two is that for DFA each input uniquely determines the state to navigate to (hence deterministic). Whereas with NFA some inputs may allow a choice of resulting states (hence non-deterministic):

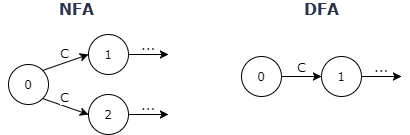
Also, DFA can change state only after reading an input, but the NFA may be constructed so that it can change state to some new state without reading any input at all. Algorithms exist to convert one type of FA into the other. NFA and DFA are equivalent in their expressive power and any DFA is a special case of an NFA.

Sometimes a scanner can run into an ambiguous situation. We know that any of the following operators =, /=, *=, += is recognized as a valid token, but how does the scanner know whether to recognize the string += as a single += token or as a + token followed by a = token? This kind of ambiguity is resolved using the longest match wins rule so the string += is recognized as one token interpreted as addition assignment operator in runtime.

Implementing DFA

The DFA can be implemented as a table-driven or hand-coded scanner. Table-driven scanners are usually generated by some specialized tools like Flex. Because with DFA each input uniquely determines the state to navigate to and it never backtracks the DFA is the preferred model for the implementation in generated scanners. The usual flow consists of converting a lexical specification (either regular grammar or regular expression) into NFA and then NFA is converted into DFA. Here is the picture that demonstrates the workflow:

However, most commercial and open-source compilers use hand-coded scanners. Such scanner is faster than a generated scanner because during implementation some overhead that is necessary in a generated scanner can be removed. That’s the type of scanner implemented in TypeScript compiler. When writing a hand-coded scanner, usually there’s no need for the explicit conversion of the grammar/regex to a DFA since it’s possible to implement the scanning algorithm manually directly from the lexical specification. Such hand-coded implementation naturally ends up working like a DFA.

Both table-driven and hand-coded scanners function in the similar way by emulating the DFA. They repeatedly read the next character in the input and emulate the DFA transition caused by that character. After reading an input the scanner checks whether there are possible transitions using the input. If a transition is found it is followed and the scanner ends up in the new state. If there are no transitions available the scanner checks if the current state is an accepting state. If that’s the case the scanner recognizes the word and returns a lexeme and its syntactic category to the calling procedure. Otherwise the scanner determines whether or not it has passed through an accepting state on the way to current state. If an accepting state has been encountered, the scanner rolls back its internal state (current character position) to that point and reports success. Otherwise it reports an error.

TypeScipt scanner implementation

TypeScript scanner implementation can be seen in the scanner.ts file. The main logic that emulates DFA by reading input and transitioning to the next state is implemented in the scan method. The gist of the implementation is an infinite while loop that checks for the input character, process all possible transitions from that character, sets the current position and returns the token class if recognized:const pos;while (true) {
tokenPos = pos;
if (pos >= end) {
return token = SyntaxKind.EndOfFileToken;
}
let ch = text.charCodeAt(pos);
switch(ch) {
case CharacterCodes.exclamation:
...
pos++;
return token = SyntaxKind.ExclamationToken;
case CharacterCodes.openParen:
...
pos++;
return token = SyntaxKind.OpenParenToken;
...

Since it emulates DFA the scanner never backtracks.

Let’s see an example. ECMAScript among others defines the following distinct punctuators :Punctuator ::
! != !== - -- -=

This rule can be easily converted into regular expressions:/!==|!=|!|--|-=|-/

and then into DFA using this tool:

Notice that all states with the exception of the start state are accepting states. This is exactly what the grammar and regular expression tell us.

TypeScript implements the above DFA as following:case CharacterCodes.exclamation:
if (text.charCodeAt(pos + 1) === CharacterCodes.equals) {
if (text.charCodeAt(pos + 2) === CharacterCodes.equals) {
pos += 3;
return token = SyntaxKind.ExclamationEqualsEqualsToken;
}
pos += 2
return token = SyntaxKind.ExclamationEqualsToken;
}
pos++;
return token = SyntaxKind.ExclamationToken;
case CharacterCodes.plus:
if (text.charCodeAt(pos + 1) === CharacterCodes.plus) {
pos += 2;
return token = SyntaxKind.PlusPlusToken;
}
if (text.charCodeAt(pos + 1) === CharacterCodes.equals) {
pos += 2
return token = SyntaxKind.PlusEqualsToken;
}
pos++;
return token = SyntaxKind.PlusToken;

As you can see from the TS implementation and DFA the scanner tries to match the longest string possible.

Handling keywords

We’ve seen already that ECMAScript defines keywords like const, let,if in its own Keyword category. One way to recognize them would be to define explicit regular expression for them and generate corresponding paths for the DFA. However, since keywords are a subset of all identifiers as defined by the grammar:Identifier:
IdentifierName but not ReservedWord

there is an alternative strategy — classify keywords as identifiers and test if an identifier is a keyword or not. This is exactly the approach used by TypeScript scanner. It keeps all keywords along with other literal tokens in the textToToken map and once the identifier is recognized it uses this map to get a correct token class which may or may not be a keyword:default:
if (isIdentifierStart(ch, languageVersion)) {
pos++;
while (isIdentifierPart(ch = text.charCodeAt(pos))) pos++;
tokenValue = text.substring(tokenPos, pos);
return token = getIdentifierToken();function getIdentifierToken(): SyntaxKind {
if (...) {
return token = textToToken.get(tokenValue);
}
return token = SyntaxKind.Identifier;

Acknowledgements

I want to say “big thanks” to sepp2k for helping me put all pieces together in my mind and providing a technical review for this article.

Also thanks to the Mohamed Hegazy for the technical review of the article related to TypeScript implementation details.

Do you want to learn more?

I’m in the process of writing the second part that explores a theory behind context-free grammar, AST construction and parser implementation algorithms. This second part will show how TypeScript parser is implemented and what algorithms it uses. Follow me to get notified whenever the article is ready.

Also here are some of the very good sources I recommend to get more information on the topics I explained here:

• Stanford CS143 (Compilers)
• Engineering: A Compiler

Thanks for reading! If you liked this article, hit that clap button below 👏. It means a lot to me and it helps other people see the story.

For more insights follow me on Twitter and on Medium.